Ap calc ab derivative practice – Embark on a captivating journey into the world of AP Calculus AB derivatives, where we unravel the intricacies of this mathematical concept and its myriad applications in the real world. From understanding the fundamentals to mastering the rules of differentiation and exploring their practical implications, this comprehensive guide will equip you with the knowledge and skills to conquer your AP Calculus AB exam.
Prepare to delve into the fascinating realm of derivatives, where we will explore their power in determining critical points, finding local extrema, and unlocking the secrets of optimization. With a treasure trove of practice problems and additional resources at your disposal, you will emerge as a master of derivative techniques, ready to tackle any challenge that comes your way.
Derivative Basics: Ap Calc Ab Derivative Practice

In mathematics, the derivative of a function measures the instantaneous rate of change of the function with respect to a variable. It is a fundamental concept in calculus and has numerous applications in various fields.
Derivatives are used to:
- Find the slope of a curve at a given point
- Determine the velocity and acceleration of an object
- Optimize functions, such as finding the maximum or minimum value
- Solve differential equations
Notations for Derivatives
The derivative of a function f(x)with respect to xcan be represented using various notations:
- f'(x)or dy/dx(Leibniz notation)
- D[f(x)]or Df(x)(operator notation)
- d f/d x(Lagrange notation)
Rules of Differentiation
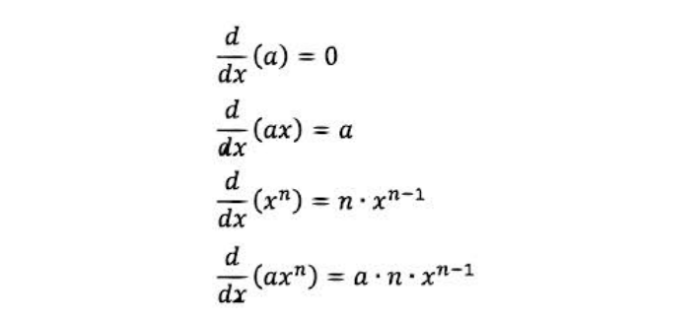
Differentiation is a mathematical operation that finds the rate of change of a function with respect to its input. It’s a fundamental tool in calculus and has various applications in fields like physics, engineering, and economics.
Power Rule
The power rule states that if f(x) = x^n, then f'(x) = nx^(n-1). For example, if f(x) = x^3, then f'(x) = 3x^2.
Product Rule
The product rule is used to differentiate the product of two functions. If f(x) = g(x) – h(x), then f'(x) = g'(x) – h(x) + g(x) – h'(x).
For instance, if f(x) = x^2 – sin(x), then f'(x) = 2x – sin(x) + x^2 – cos(x).
Quotient Rule
The quotient rule is applied when differentiating the quotient of two functions. If f(x) = g(x) / h(x), then f'(x) = [(g'(x) – h(x)) – (g(x) – h'(x))] / h(x)^2.
Practice makes perfect when it comes to mastering AP Calc AB derivatives. If you’re looking to brush up on your skills, check out the CRCST practice test chapter 3 for some challenging problems. After tackling those, you’ll be well-prepared to conquer any derivative that comes your way in AP Calc AB.
For example, if f(x) = x^3 / (x^2 + 1), then f'(x) = [(3x^2 – (x^2 + 1)) – (x^3 – 2x)] / (x^2 + 1)^2.
Chain Rule, Ap calc ab derivative practice
The chain rule is used to differentiate composite functions. If f(x) = g(h(x)), then f'(x) = g'(h(x)) – h'(x).
For instance, if f(x) = sin(x^2), then f'(x) = cos(x^2) – 2x.
Applications of Derivatives

Derivatives have numerous applications in various fields, including mathematics, science, and economics. One of the most important applications of derivatives is finding critical points, which are points where the derivative is zero or undefined. Critical points can be used to find local extrema (maximum or minimum values) of a function.
Methods for Finding Local Extrema
There are several methods for finding local extrema:
- First Derivative Test: If the first derivative of a function is positive at a point, the function is increasing at that point. If the first derivative is negative, the function is decreasing. Local extrema can occur at points where the first derivative changes sign.
- Second Derivative Test: If the second derivative of a function is positive at a point, the function is concave up at that point and the point is a local minimum. If the second derivative is negative, the function is concave down and the point is a local maximum.
Comparison of First and Second Derivative Tests
The following table compares the first and second derivative tests:
| Test | Condition | Conclusion |
|---|---|---|
| First Derivative Test | f'(x) = 0 or f'(x) does not exist | Possible local extremum |
| Second Derivative Test | f'(x) = 0 and f”(x) > 0 | Local minimum |
| Second Derivative Test | f'(x) = 0 and f”(x) < 0 | Local maximum |
Practice Problems

To solidify your understanding of differentiation rules, let’s dive into a series of practice problems that will test your skills.
These problems are designed to cover various differentiation techniques, from the fundamental power rule to the more complex chain rule. By working through these exercises, you will not only enhance your problem-solving abilities but also gain a deeper comprehension of the concepts.
Power Rule
- Find the derivative of f(x) = x 5.
- Differentiate g(x) = 2x 3+ 5x 2– 1.
- Determine the derivative of h(x) = (x 2– 1) 3.
Product Rule
- Find the derivative of f(x) = (x + 2)(x – 1).
- Differentiate g(x) = x 2sin(x).
- Determine the derivative of h(x) = (2x + 1) 3(x 2– 5).
Quotient Rule
- Find the derivative of f(x) = (x 2+ 1) / (x – 2).
- Differentiate g(x) = sin(x) / cos(x).
- Determine the derivative of h(x) = (x 3– 2x) / (x 2+ 1).
Chain Rule, Ap calc ab derivative practice
- Find the derivative of f(x) = sin(2x).
- Differentiate g(x) = (x 2+ 1) 5.
- Determine the derivative of h(x) = ln(x 2– 3).
Additional Resources
In addition to the resources already provided, the following links, textbooks, and websites can be helpful for further practice and exploration of AP Calculus AB derivatives.
Online Resources
Online resources provide a convenient and interactive way to practice derivative concepts. Here are some links to websites that offer a variety of exercises, simulations, and tutorials:
- Khan Academy: https://www.khanacademy.org/math/ap-calculus-ab/ab-derivatives
- Purplemath: https://www.purplemath.com/modules/derivintro.htm
- CalcChat.com: https://www.calcchat.com/calculus/derivatives
- PatrickJMT: https://www.patrickjmt.com/calculus/ab-derivatives
- Mathway: https://www.mathway.com/calculus/derivative
Textbooks
Textbooks provide a comprehensive overview of AP Calculus AB derivatives, including explanations, examples, and practice problems. Here are some popular textbooks that cover this topic:
- Calculus: Early Transcendentals by James Stewart
- Calculus for the AP Course by Michael Sullivan
- AP Calculus AB by Larson and Edwards
- Calculus and Its Applications by Bittinger, Ellenbogen, and Surgent
- Calculus: A Complete Course by Adams and Essex
Interactive Simulations and Tutorials
Interactive simulations and tutorials allow students to visualize and explore derivative concepts in a dynamic way. Here are some websites that offer such resources:
- Desmos: https://www.desmos.com/calculator/ddw6zznw6i
- GeoGebra: https://www.geogebra.org/m/gfhg4mkh
- Wolfram Alpha: https://www.wolframalpha.com/examples/calculus/derivatives
- Symbolab: https://www.symbolab.com/derivative-calculator
- Integral-Calculator: https://www.integral-calculator.com/derivative
Key Questions Answered
What is the significance of derivatives in real-world applications?
Derivatives play a crucial role in fields such as physics, engineering, economics, and optimization. They allow us to determine the rate of change of various quantities, model complex systems, and solve problems involving motion, growth, and decay.
How can I effectively practice derivative techniques?
Regular practice is essential for mastering derivative techniques. Utilize the practice problems provided in this guide and seek additional problems from textbooks, online resources, and past exam papers. Consistent practice will enhance your problem-solving skills and build your confidence.
What are some common mistakes to avoid when working with derivatives?
Common pitfalls include applying the rules of differentiation incorrectly, forgetting to use the chain rule when necessary, and making algebraic errors. Careful attention to detail and a thorough understanding of the concepts will help you avoid these mistakes.