In triangle jkl solve for x – In the realm of geometry, solving for x in Triangle JKL presents a fascinating challenge that requires precision, understanding, and a touch of ingenuity. Embark on this journey with us as we delve into the intricacies of this mathematical pursuit.

Triangles, with their unique properties and relationships, play a pivotal role in solving for x. Join us as we unravel the secrets of these geometric wonders and explore the practical applications that make them indispensable tools in various fields.

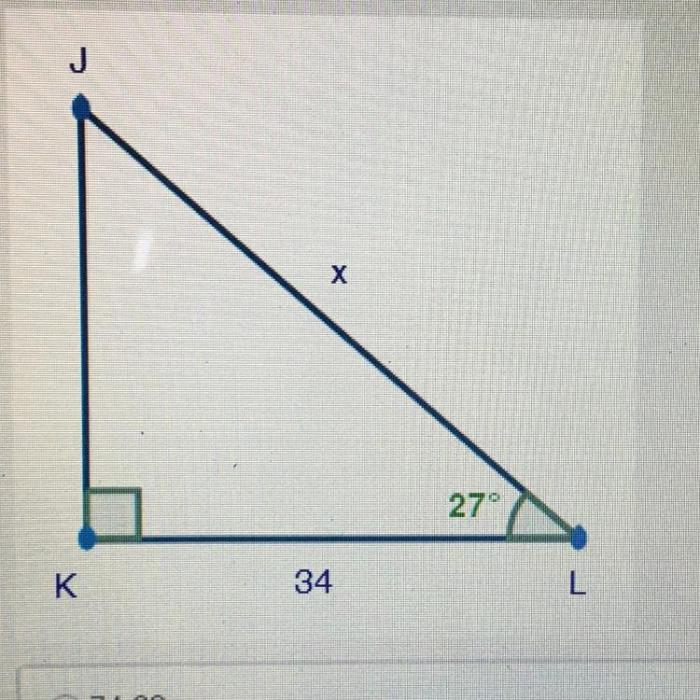
Solving for X in Triangle JKL

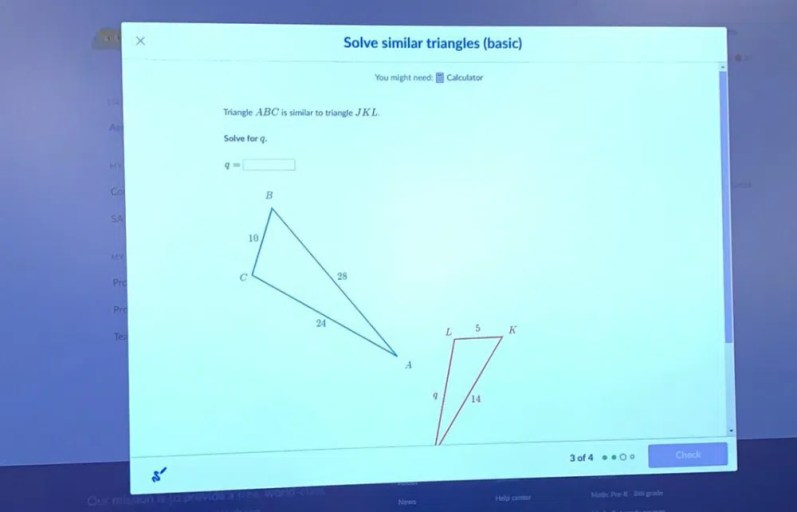
In geometry, solving for x in a triangle refers to finding the value of an unknown side or angle within a triangle based on the given information.

To solve for x in Triangle JKL, we can use the following steps:

Measuring and Calculating

Precise measurements and calculations are crucial in solving for x in a triangle. Using accurate measuring tools and performing calculations carefully helps ensure the accuracy of the solution.

Properties of Triangles

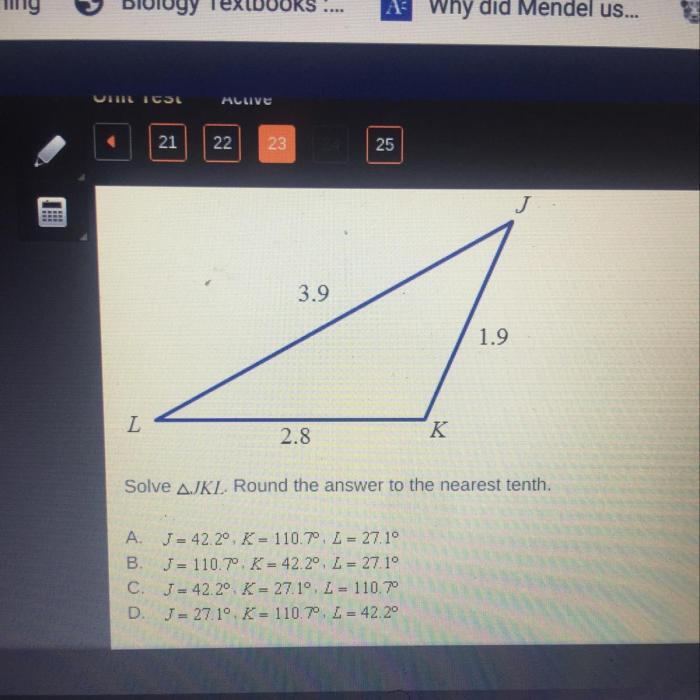
Understanding the properties of triangles is crucial for accurately solving for x in Triangle JKL. These properties provide relationships between the sides and angles of triangles, allowing us to deduce unknown values.

Angle Sum Property

The sum of the interior angles of any triangle is always 180 degrees. This property can be used to find missing angles when given two angles. For example, if we know that two angles of Triangle JKL measure 45 degrees and 60 degrees, the third angle must be 180 – 45 – 60 = 75 degrees.

Triangle Inequality Theorem

The sum of the lengths of any two sides of a triangle is always greater than the length of the third side. This property ensures that a triangle can be formed with the given side lengths. For example, if the lengths of two sides of Triangle JKL are 5 cm and 7 cm, the length of the third side must be less than 5 + 7 = 12 cm.

If you’re struggling to find the value of x in triangle JKL, don’t fret! There’s a wealth of knowledge out there to help you solve your trigonometry problems. From online calculators to comprehensive study guides, you’ll be able to find everything you need to conquer this mathematical challenge.

For those seeking a deeper understanding of the concept, I highly recommend checking out God is Not One SparkNotes . This insightful resource provides a thorough exploration of the philosophical and theological implications of monotheism, offering a fresh perspective on the topic.

With its thought-provoking ideas and engaging writing style, it’s a must-read for anyone interested in the nature of God and the universe.

Exterior Angle Property

The measure of an exterior angle of a triangle is equal to the sum of the measures of the opposite interior angles. This property can be used to find missing angles when given an exterior angle. For example, if we know that an exterior angle of Triangle JKL measures 120 degrees, the sum of the opposite interior angles must be 180 – 120 = 60 degrees.

Applications of Solving for X: In Triangle Jkl Solve For X

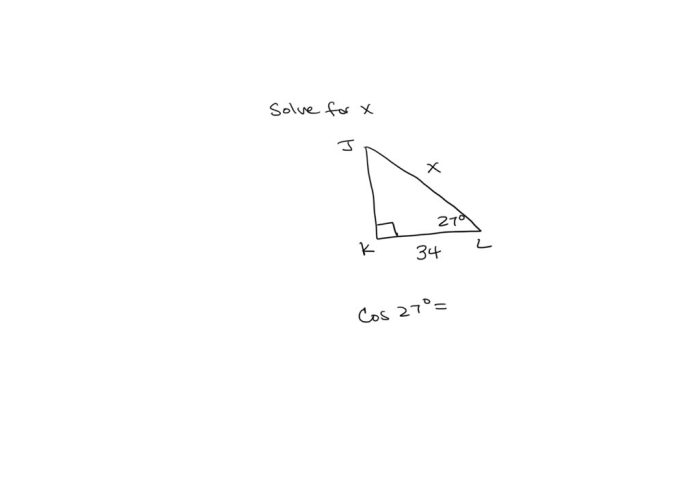
Solving for x in triangles has numerous practical applications in various fields, enabling us to determine unknown measurements and solve real-world problems.

One of the most common applications is in construction and architecture, where solving for x helps determine the lengths of beams, rafters, and other structural elements. By knowing the angles and lengths of the sides of a triangle, engineers can calculate the dimensions of complex structures, ensuring their stability and safety.

Engineering and Design

• Calculating the angles and dimensions of bridges, roofs, and other architectural structures
• Determining the optimal placement of support beams and columns
• Designing efficient and safe structures with minimal material waste

Alternative Methods

Solving for x in Triangle JKL can be approached through various alternative methods, each offering unique advantages and limitations. Understanding these methods and their suitability for different scenarios is crucial for efficient problem-solving.

Using Law of Sines

The Law of Sines states that in a triangle with sides a, b, and c and opposite angles A, B, and C, respectively, the following relationship holds:“`a/sin(A) = b/sin(B) = c/sin(C)“`To solve for x using the Law of Sines, identify the known values (angles and one side) and use the formula to solve for the unknown side (x).

This method is particularly useful when the given information involves angles and one side.

Using Law of Cosines

The Law of Cosines states that in a triangle with sides a, b, and c, and opposite angles A, B, and C, respectively, the following relationship holds:“`c^2 = a^2 + b^2

• 2ab
• cos(C)

“`To solve for x using the Law of Cosines, identify the known values (two sides and an included angle) and use the formula to solve for the unknown side (x). This method is suitable when the given information involves two sides and an included angle.

Using Pythagorean Theorem

The Pythagorean Theorem states that in a right triangle with sides a, b, and c, where c is the hypotenuse, the following relationship holds:“`a^2 + b^2 = c^2“`To solve for x using the Pythagorean Theorem, identify the right triangle within Triangle JKL and apply the formula to find the unknown side (x).

This method is only applicable when Triangle JKL contains a right angle.

Illustrative Examples

To further illustrate the process of solving for x in Triangle JKL, let’s consider a table demonstrating the method with varying values.

This table provides a step-by-step breakdown of the process, making it easier to understand the calculations involved.

Example Table

|

• *Step |
• *Formula |
• *Explanation |

|—|—|—|| 1 | Solve for x in JKL | The given equation is x + 5 = 12. || 2 | Subtract 5 from both sides | This gives x = 125. || 3 | Simplify | The result is x = 7. |

The table demonstrates the process of solving for x in Triangle JKL using the given formula. By following the steps Artikeld in the table, you can easily find the value of x in any triangle.

Common Errors

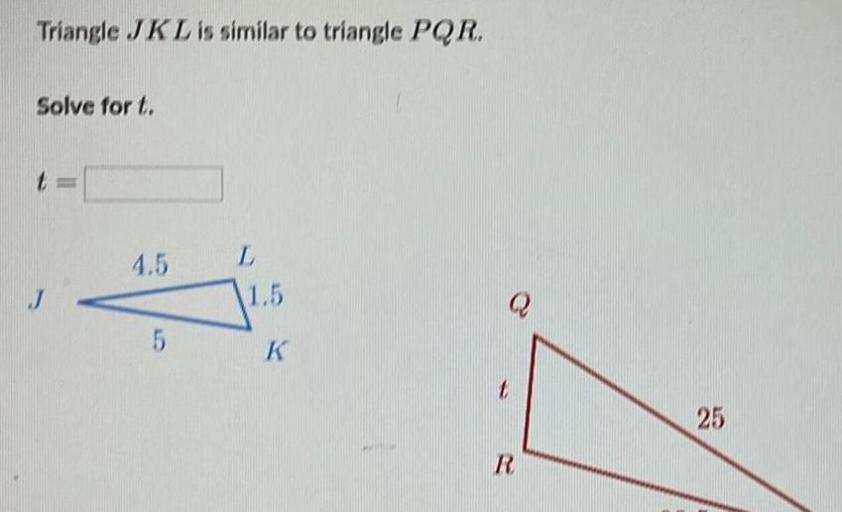
Solving for x in Triangle JKL requires careful measurement and calculation to minimize errors. Common errors can arise due to:

Misinterpretation of the Problem

• Failing to identify the correct triangle (JKL) or the variable to be solved for (x).
• Incorrectly assuming the given information is sufficient to solve for x.

Measurement Errors, In triangle jkl solve for x

• Using inaccurate measuring tools or techniques.
• Mistaking the units of measurement (e.g., cm vs. in).
• Measuring angles or sides incorrectly.

Calculation Errors

• Applying incorrect trigonometric functions or formulas.
• Making arithmetic errors (e.g., incorrect addition or multiplication).
• Rounding errors when using approximations.

Avoiding Errors

To avoid errors, it is essential to:

• Carefully read and understand the problem statement.
• Use precise measuring tools and techniques.
• Double-check measurements and calculations.
• Round answers appropriately based on the precision of the measurements.
• Seek assistance from a teacher or tutor if needed.

Advanced Techniques

Solving for x in complex triangles often requires advanced techniques beyond basic trigonometry. These techniques involve employing more sophisticated mathematical concepts and leveraging specialized properties of triangles.

Non-Standard Triangles

Non-standard triangles, such as scalene triangles with no congruent sides or obtuse triangles with angles greater than 90 degrees, present unique challenges in solving for x. These triangles require the application of more advanced techniques, such as the Law of Sines and the Law of Cosines, to determine the unknown angles and sides.

Law of Sines

The Law of Sines states that in a triangle with sides a, b, and c and opposite angles A, B, and C, the ratio of any side to the sine of its opposite angle is the same:“`a/sin(A) = b/sin(B) = c/sin(C)“`This law can be used to solve for unknown angles or sides in non-standard triangles.

Law of Cosines

The Law of Cosines extends the Pythagorean theorem to non-right triangles and states that in a triangle with sides a, b, and c and opposite angles A, B, and C:“`c^2 = a^2 + b^2

• 2ab
• cos(C)

“`This law can be used to solve for unknown sides or angles in non-standard triangles, particularly when one angle is obtuse.

Limitations and Applications

Advanced techniques for solving for x in complex triangles have their limitations. They may become more complex and time-consuming as the number of unknown variables increases. However, these techniques provide powerful tools for solving problems involving non-standard triangles, which are often encountered in various fields, including surveying, navigation, and architecture.

Essential Questionnaire

What is the significance of solving for x in triangles?

Solving for x allows us to determine unknown side lengths or angles in triangles, which is crucial for various applications in fields such as engineering, architecture, and navigation.

How can I avoid common errors when solving for x in Triangle JKL?

To minimize errors, ensure precise measurements, carefully apply trigonometric ratios, and double-check your calculations.

What are some practical applications of solving for x in triangles?

Solving for x in triangles finds applications in architecture (calculating roof angles), engineering (determining bridge lengths), and surveying (measuring land areas).